Sunday, March 25, 2007
ClusTree: The Hierarchical Clustering Analyzer (Version 0.8)
By
Outline
ClusTree is a
ClusTree is a two-step wizard that envelops some basic Matlab clustering methods and introduces the Top-Down Quantum Clustering algorithm.
ClusTree provides a flexible and customizable interface for clustering data with high dimensionality.
ClusTree allows both textual and graphical display for the clustering results.
ClusTree can either apply hierarchical clustering to a dataset or analyze ‘pre-clustered’ results.
ClusTree is a self-extracting package. In
order to install and run the ClusTree
tool, follow these three easy steps:
1. Download the
ClusTree.zip packaged to your local drive[2].
2. Add the ClusTree destination directory to your Matlab path.
3. Within Matlab, type 'clustree' at the command prompt.
Upon typing 'clustree' at the command prompt the main window is open.
1. ClusTree: Main
window
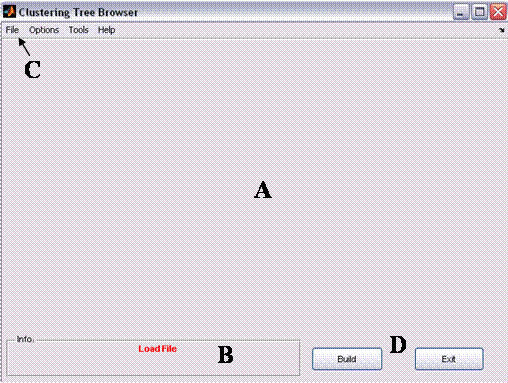
Figure 1: Clustree's main window
The main window consists of four areas:
A. Graphical window –
the area in which the clustering result (i.e., the tree) is displayed. When no
tree is loaded (e.g., prior the clustering) this area is empty.
B. Information Bar – the area in which the status is displayed (e.g., when no data is loaded a red ‘Load file’ indication is displayed). When a tree is loaded and the external classification is available (see Tree Options below) , three clustering scores are displayed (see ý1.2.i belowBranch information
By selecting a
tree branch, a tooltip floating window appears (Figure 5). The tooltip displays
the Branch id, number of elements it includes, and the significance enrichment p-values.
The list of elements that belong to the selected branch can be exported using
the export command (see ‘Export current’ below)
Scoring the Tree
above).
C. Menus Bar– the area
in which the some actions re available: examples are data loading, data
processing, display options, detailed evaluation options etc.
D. Command Buttons – 2
main buttons: ‘Build’ – build a tree option (applicable only after clustering
is applied) and ‘Exit’ – safely exiting the application.
1. New clustering
/Open ‘pre-clustered’ data
ClusTree can either cluster a given dataset or visualize and analyze a dataset that has already been clustered
i.
New clustering
ClusTree receives three input parameters, which are Matlab base workspace variables (i.e., must be defined in Matlab workspace before running the ClusTree).
·
Data (Mandatory field) - two-dimensional matrix
of doubles. Represents the elements (objects to be clustered are the matrix’s columns).
·
Real classification (Optional
field) - one-dimensional vector. Represents the real classification of the
elements (i.e., the class of the i-th element appears in the i-th
place in the vector). Therefore, the vector’s length must be equal to the
number of elements in the Data matrix (an error occurs otherwise).
The
two input parameters can be either typed in or selected from the base
workspace.
·
Clustering Algorithms (Agglomerative,
TDQC, PDDP)
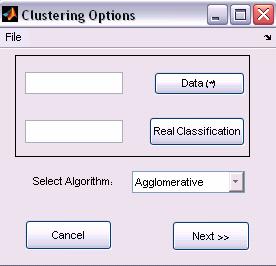
Figure 2: New Clustering options
1. Agglomerative
Clustering
The Bottom-Up Agglomerative clustering algorithm is the default option of the Matlab environment (See Matlab, Statistics Toolbox 5.1 manual.
User should specify the data representation, Distance measure and Linkage type options.
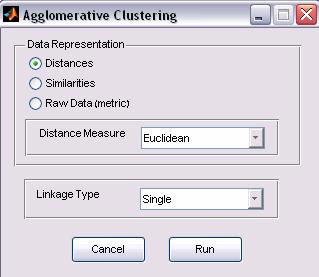
Figure 3: Agglomerative Clustering options
a. Data
Representation
The input data matrix can be represented in various ways
a. Distances: a symmetric squared matrix in which the value in the ij place represents the distance between elements i and j.
b. Similarities: a symmetric squared matrix in which the value in the ij place represents the similarity between elements i and j.
c. Raw Data: a features space matrix, which the value in the ij place represents the value of feature j for elements i.
The user should specify in which of the three options the data is represented. If the data representation is either Distances or Similarity, the Distance Measure option is disabled and ignored. Otherwise (Raw data), the user should select one of the Distance Measure options.
b. Distance Measure
1.
euclidean
2.
seuclidean
3.
cityblock
4.
mahalanobis
5.
minkowski
6.
cosine
7.
correlation
8.
hamming
9.
jaccard
10.
chebychev
c. Linkage Type
After the distance is measure, a linkage is applied. The Linkage types are:
1.
single
2.
complete
3.
average
4.
weighted
5.
centroid
6.
median
7.
ward
2. Top-Down-Quantum-Clustering
(TDQC) Options
The
TDQC options
can be specified in a configuration file (advanced mode), or by setting the
parameters.
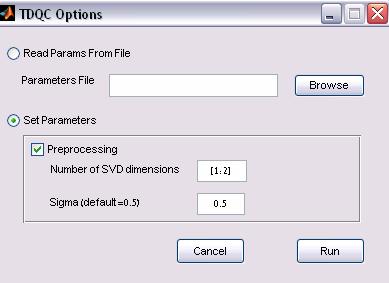
Figure 4: TDQC Clustering options
a. Parameter file
option
The TDQC can be applied to a configuration input file. The input file
format is as follows
![Text Box: % A line that starts with a ‘%’ is a comment
% data=[m*n data matrix] * mandatory
data=x
%realmapping=[1*n classification] – optional
realmapping=y
%preprocessing= [0-no, 1 - SVD, 2 - SVD + normalization]
preprocessing=2
% algorithm=4 --> must remain constant!
algorithm=4
%dims=[start:end]--> dimensions
dims=[1:2]
%clustercolumns=1 --> must remain constant!
clustercolumns=1
%steps=[for gradient descend]
steps=50
%numelems=[ number of elements]
numelems=200
%Sigma=[for qc]
Sigma=0.5](Clustree_files/image010.gif)
b. Direct input
option
1. Preprocessing –
whether to cluster normalized, truncated SVD vectors (selected by default)
2. Sigma value – the
Parzen window size (default is 0.5).
3. PDDP Clustering
(when installed)
Once the algorithm is chosen and applied, the status message in the information bar is changed to ‘loaded’
ii.
Open previously saved results
Browsing previously saved file. The file is a Matlab data file (.mat) with two parameters: parent (required) and realClass (optional)
·
parent
an (m-1)-by-3 matrix. The output of the Matlab ‘linkage’ function. parent
is an containing cluster tree information. The leaf nodes in the cluster
hierarchy are the objects in the original data set, numbered from 1 to m. They
are the singleton clusters from which all higher clusters are built. Each newly
formed cluster, corresponding to row i in parent, is assigned the index m+i, where
m is the total number of initial leaves. Columns 1 and 2, parent (i,1:2), contain
the indices of the objects that were linked in pairs to form a new cluster. This
new cluster is assigned the index value m+i. There are m-1 higher clusters that
correspond to the interior nodes of the hierarchical cluster tree. Column 3, parent
(i,3), contains the corresponding linkage distances between the objects paired
in the clusters at each row i.
Note:
ClusTree ignores
the 3rd column (the linkage distances).
·
realClass
(Optional field) - one-dimensional vector. Represents the real
classification of the elements (i.e., the class of the i-th element
appears in the i-th place in the vector). Therefore, the vector’s length
must be equal to the number of elements in the Data matrix (an error occurs
otherwise).
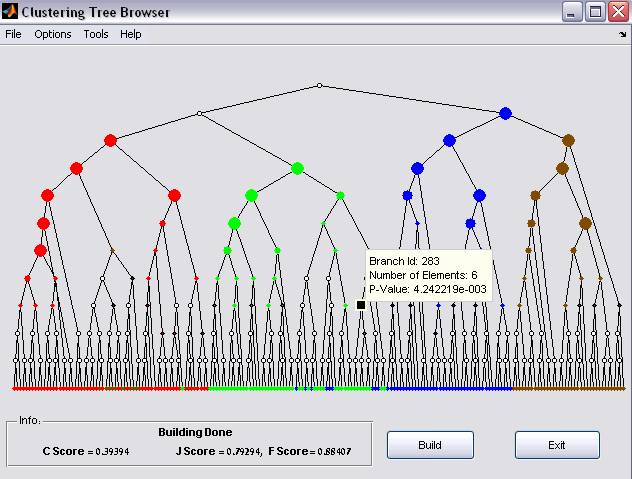
Figure 5: Clustering results Dot sizes indicate statistical
enrichment levels (larger sizes correspond to smaller p-values). Uncolored
nodes represent non-significant enrichment
The clustering tree represents a parent-child relation in which the leaf nodes represent data-elements and tree branched represent a cluster (that includes the nodes below).
If the real classification information is available
and paint level is set to branches (see ý3 below), clustering evaluation can be presented. Since each node
specifies a cluster, enrichment p-values can be calculated to assign the
given node with one of the classes in the
data. This is done by using the hypergeometric probability density function. The significance p-value
of observing k elements assigned by the algorithm to a given category
in a set of n elements is given by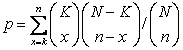
, where K is the total number of elements assigned
to the class (the category) and N is the number of elements in the
dataset. The p-values for all nodes and all classes may be viewed as
dependent set estimations; hence we apply the False Discovery Rate (FDR) criterion
to them requiring q<0.05 [1]. P-values that do not
pass this criterion are considered non-significant. We further apply another
conservative criterion; namely, a node is considered significant only if k≥n/2
(i.e., the majority of its elements belongs to the enriched category).
In the graphical results, Dot sizes indicate statistical enrichment levels (larger sizes correspond to smaller p-values). Uncolored nodes represent non-significant enrichment (for modifications of the above configurations see ý3 below).
By
selecting a tree branch, a tooltip floating window appears (Figure 5). The tooltip displays the Branch id, number of
elements it includes, and the significance enrichment p-values. The list
of elements that belong to the selected branch can be exported using the export
command (see ‘Export
current’ below)
ii.
Scoring the Tree
1. C Score –
the relative number of significant branches (clusters) [#significant branches/ the
# of branches
in the tree]
2. J Score We
define the weighted best-J-Sc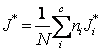ore (
) where J*i is the best
J-Score (
where tp is the number of true positive cases, fn
the number of false negative cases and fp the number of false positive
cases), for class i in the tree, ni is the number
of datapoints in class i, c is the number of classes and N is the
number of datapoints in the dataset. This criterion provides a single
number specifying the quality of the tree based on a few nodes that contain
optimal clusters.
3.
F
Score – similarly to the J Score, the weighted best-F-Score (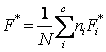
)
where F*i is the best F-Score (
where 
and 
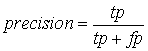),for class i in the tree, ni is
the number of datapoints in class i,
c is the number of classes and N is the
number of datapoints in the dataset
3. Analyze the tree –
in addition to the visualization and scoring options, ClusTree provides
additional analysis tools (scores Distribution and Ultrametric Display)
i.
Scores Distribution
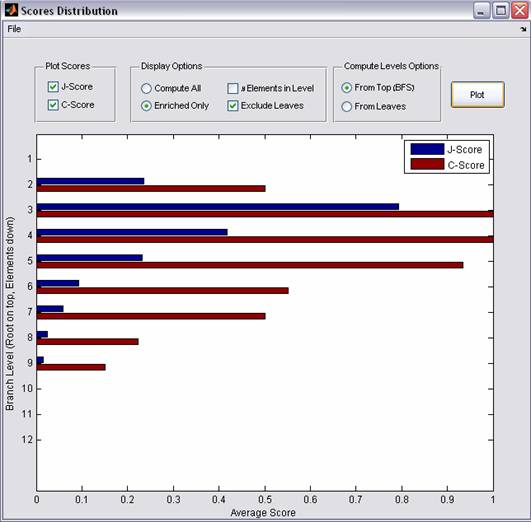
Figure 6: Visualization
Scores Distribution
The Scores Distribution displays the Levels scores. A level l of the tree contains all nodes that are separated by l edges from the root, i.e., that share the same Breadth First Search (BFS) mapping. Each level specifies a partition of the data into clusters. Choosing for each node, the class for which it turned out to have a significant node score, we evaluate its J-score (see avove). If the node in question has been judged to be non-significant by the enrichment criterion, its J-score is set to null. The level score is defined as the average of all J-scores at the given level.
In addition to the above definitions, the Levels C scores can be displayed and some modifications can be applied (displaying the number of branches in each level, including non-significant branches and computing levels from leaf nodes instead of from the root, see Figure 6)
ii.
Ultrametric Display
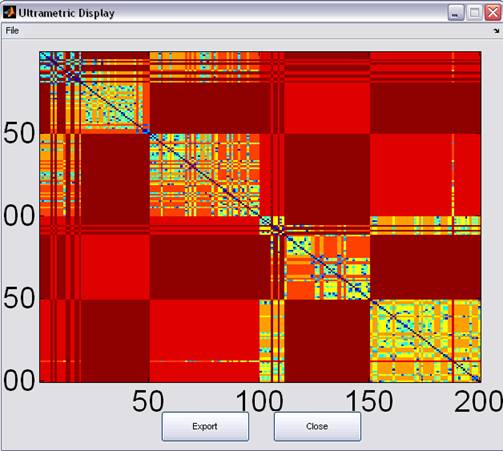
Figure 7: Ultrametric Display
The resulting tree defines an Ultrametric dimension, where the distance between two leaf-nodes is defined as the number of edges connecting them.
The Ultrametric information is graphically displayed and can be exported in a textual format.
1. Export current
branch
If a branch is selected (see Branch information above and Figure 5), its properties can be exported to either a set of Matlab variables or to a text file.
2.
Print graphical information – printing the
graphical results of the clustering (i.e., the tree)
3. Save current results – save the current environment for future analysis (output file can be served as an input file, see ‘Open previously saved results’ above)
4. Visualization
Options
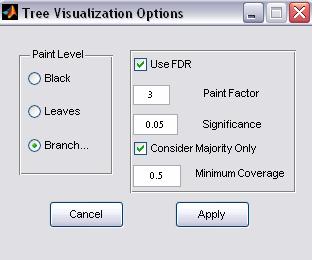
Figure 8: Visualization options
ClusTree allows the configuration of the default visualization settings.
a. Paint Level
i. Black – regardless if the real classification is available or not, the tree is displayed as black (i.e., nodes and branches are not colored). If this option is selected all clustering evaluation information is not available.
ii. Leaves (applicable only if real classification is available) - leaf nodes are colored according to their classification association
iii. Branches (default) - (applicable only if real classification is available) – both leaf nodes and branches are colored (for more information, see ý2 above).
b. FDR (False
Discovery Rate) Option
The p-values
for all nodes and all classes may be viewed as dependent set estimations; hence
we suggest applying the False Discovery Rate (FDR) criterion to them. Nevertheless,
if user prefers not to apply FDR correction, the FDR option should be
unselected.
c. Paint Factor
The number indicates the relative size of the nodes size. Note: This option is for visualization purposes only.
d. Significance
The p-value threshold for specifying a significant branch
e.
Majority Consideration
If this option is checked, the user can specify a coverage threshold for coloring a branch (values range from 0 to 1). For example if the user specifies 0.5, A branch is considered significant only more than 50% of its elements belong to the enriched cluster. Note: the value 1 means a ‘complete homogeneity’ (i.e., all the elements in every colored branch belong to the enriched cluster)
5.
Optional extensions
ClusTree is a set of self explanatory and documented Matlab functions and as such can be extended. Users that are familiar with Matlab and wish to change features in the current tool are welcome to do so. In addition, we designed this tool that adding a new clustering method is done by changing only one function.
1. Project name: ClusTree: The Hierarchical Clustering Analyzer
2. Project home page: http://adios.cs.tau.ac.il/ClusTree/clustree, http://www.protonet.cs.huji.ac.il/ClusTree/clustree (alternative)
3. Operating system(s): Platform independent tested on MS-Windows (2000, XP), Linux and Unix
4.
Programming
language: Matlab
5.
Other
requirements: Matlab 7 or higher, Statistics Toolbox 5.1, COMPACT, and the PDDP
package (optionally, should be downloaded separately from http://www-users.cs.umn.edu/~boley/PDDP.html)
6. License: Matlab
7. Any restrictions to use by
non-academics: currently open for all academic users. Adequate
referencing required. Non-academic users are required to apply for permission
to use this product.
[1]
Benjamini, Y. and Hochberg, Y. Controlling the False
Discovery Rate: A Practical and Powerful Approach to Multiple Testing. Journal
of the Royal Statistical Society. Series B (Methodological), 57 (1). 1995, 289-300.